隐马尔可夫模型
HMM(Hidden Markov Model)是一个生成式模型,X为观测序列,Y为隐序列。基于HMM的两个假设:
- 齐次马尔科夫假设,即假设隐藏的马尔科夫链在任意时刻t的状态只依赖于其前一时刻的状态,与其他时刻的状态及观测无关,也与时刻t无关;
- 观测独立性假设,即假设任意时刻的观测只依赖于该时刻的马尔科夫链的状态,与其他观测和状态无关。
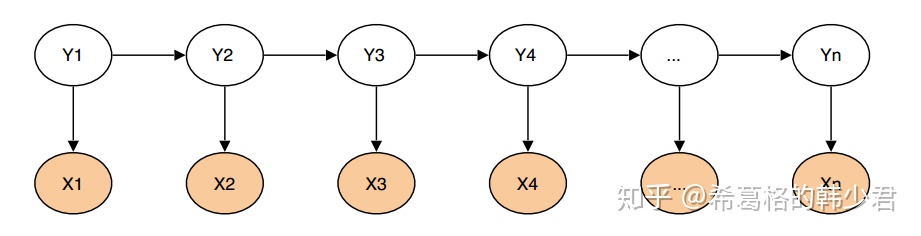
HMM中的五元组表示:
- 观测序列
- 隐藏状态序列
- 状态初始概率
- 状态转移概率
- 状态发射概率
模型的表达:P(X,Y)=P(y_0)P(x_0|y_0)\prod_{t=1}^nP(y_t|y_{t-1})P(x_t|y_t)
P(y_0)是状态初始概率,P(y_t|y_{t-1})是状态转移概率,P(x_t|y_t)是状态发射概率
HMM的三个基本问题:
- 概率计算问题,HMM的五元组,在模型下给定隐藏序列Y,计算观测序列X出现的概率也就是Forward-backward算法
- 学习问题,已知观测序列X,隐藏序列Y,估计模型的状态初始概率,状态转移概率和状态发射概率,使得再该模型下观测序列X的概率尽可能得大,即用极大似然估计的方法估计参数
- 预测问题,也称为解码问题,已知模型状态初始概率,状态转移概率和状态发射概率和观测序列Y,求最大概率的隐藏序列Y。
参考链接:Jieba分词原理解析
创建于2023.3.17/0.3,修改于2023.3.17/0.3