衡量机器学习算法好坏的指标
一、分类
1.精确率与召回率
精确率与召回率多用于二分类问题。精确率(Precision)指的是模型判为正的所有样本中有多少是真正的正样本;召回率(Recall)指的是所有正样本有多少被模型判为正样本。设模型输出的正样本集合为\(A\),真正的正样本集合为\(B\),则有:\[Precision(A,B)={\left|\right| A\bigcap B\left|\right| \over \left|\right| A\left|\right|},Recall(A,B)={\left|\right| A\bigcap B\left|\right|\over\left|\right| B\left|\right|}\]
有时候我们需要在精确率与召回率间进行权衡,一种选择是画出精确率-召回率曲线(Precision-Recall Curve),曲线下的面积被称为AP分数(Average precision score);另外一种选择是计算\(F_\beta\)分数:\[F_\beta=(1+\beta^2)\cdot{precision\cdot recall\over\beta^2\cdot precision+recall}\]。当\(\beta=1\)称为\(F_1\)分数,是分类与信息检索中最常用的指标之一。
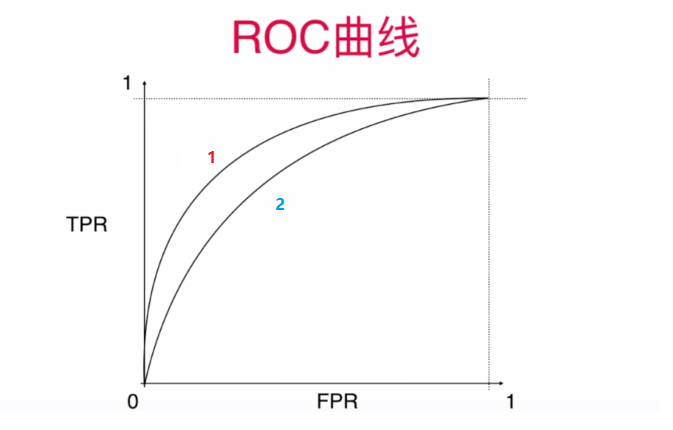
2.ROC
在信号检测理论中,接收者操作特征曲线(receiver operating characteristic curve)是一种坐标图式的分析工具。
设模型输出的正样本集合为\(A\),真正的正样本集合为\(B\),所有样本集合为\(C\),我们称\(\left|\right| A\bigcap B\left|\right|\over\left|\right| B\left|\right|\)为真正率(True-positive rate),\(\left|\right| A-B\left|\right|\over\left|\right| C-B\left|\right|\)为假正率(False-positive rate)。
ROC曲线适用于二分类问题,是以假正率为横坐标,真正率为纵坐标的曲线图。ROC有个很好的特性:当测试集中的正负样本的分布变化时,ROC曲线能够保持不变。在实际的数据集中经常会出现类不平衡(class imbalance)现象,即负样本比正样本多很多(或者相反)
我们想像这样一种场景,接触阳性样本给我们带来“收益”,接触阴性样本给我们造成“成本”,如果接触样本中的一个阳性样本,收益是1,接触样本中的一个阴性样本,成本也是1,不接触样本,既不产生收益也不产生成本。自然地,如果不使用分类器接触所有样本,总的收益是1-1=0;若使用分类器决定是否接触样本,分类器预测为阳,就去接触样本,分类器预测为阴,不去接触。因为不接触样本不会产生收益或成本,所以只需要看分类器预测为阳的样本。预测为阳的样本中,TP将产生TPR的收益,FP将产生FPR的成本。那么一个分类器的分类效果对应ROC空间的一个点
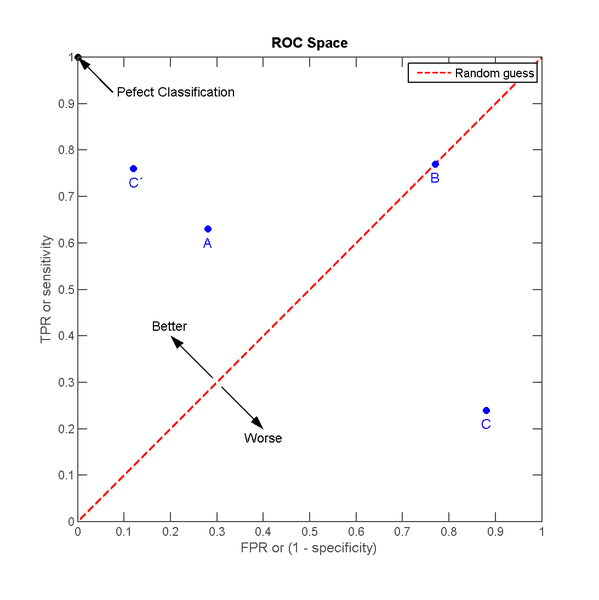
A, B, C三个点分别代表三个不同的分类器对同样的样本作预测的结果。最好的方法是A,因为他的收益大于成本(TPR>FPR),最差的是C(TPR<FPR),中等的是B,相当于随机分类器。若把C以(0.5, 0.5)为中点作一个镜像,得到C',C'的效果比A好。C'相当于一个与C预测结果完全相反的分类器。
实际的应用中,分类器还会给出它预测某个样本为阳的概率,并且有一个事先给定的门槛值(threshold),概率高于threshold的预测为阳,低于threshold的预测为阴。假设以下是某个分类器对id为1-10的客户的分类结果:
| id | probability of 1 | true class |
|---|---|---|
| 1 | 0.9 | 1 |
| 2 | 0.88 | 1 |
| 3 | 0.86 | 0 |
| 4 | 0.84 | 1 |
| 5 | 0.82 | 1 |
| 6 | 0.7 | 1 |
| 7 | 0.65 | 0 |
| 8 | 0.5 | 1 |
| 9 | 0.4 | 0 |
| 10 | 0.1 | 0 |
如果我们把threshold定为0.5,接触id为1~8的客户,此时TPR=TP/所有真实值为阳性的样本个数=6/6=1,FPR=FP/所有真实值为阴性的样本个数=2/4=0.5
同理,如果我们把threshold定为0.8,接触id为1~5的客户,此时TPR=TP/所有真实值为阳性的样本个数=4/6=0.67,FPR=FP/所有真实值为阴性的样本个数=1/4=0.25
这两个threshold及分析对象分别对应ROC空间中的两点
上面的例子当中,共有10笔预测数据,则共有11钟threshold的设定方法,每一个threshold对应ROC空间的一个点,把这些点连接起来,形成ROC曲线。数据量小的情况下,曲线是一折一折的,数据量大的时候,看起来才像“曲线”
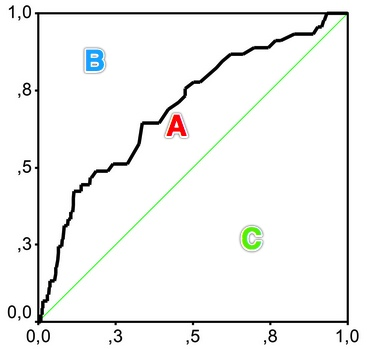
AUC分数是曲线下的面积(Area under curve),越大意味着分类器效果越好。使用AUC来衡量分类模型的好坏,可以忽略由于threshold的选择所带来的影响,因为实际应用中,threshold常常由先验概率或是人为决定的。
基尼系数是指ROC曲线和中线围成的面积与中线之上面积的比例,如图所示计算\[gini=A/(A+B)=(AUC-C)/(A+B)=(AUC-0.5)/0.5=2*AUC-1\]
3.对数损失
对数损失(Log loss)亦被称为逻辑回归损失(Logistic regression loss)或交叉熵损失(Cross-entropy loss)。
对于二分类问题,设\(y\in \{ 0,1\}\)且\(p=Pr(y=1)\),则对每个样本的对数损失为:\[L_{log} (y,p)=-log\ Pr(y\left|\right| p)=-(y\ log(p)+(1-y)\ log(1-p))。\]可以很容易地将其扩展到多分类问题上。设\(Y\)为指示矩阵,即当样本\(i\)的分类为\(k\)时\(y_{i,k}=1\);设\(P\)为估计的概率矩阵,即\(p_{i,k}=Pr(t_{t,k}=1)\),则对每个样本的对数损失为:\[L_{log}(Y_i,P_i)=-log\ Pr(Y_i\left|\right| P_i)=\sum_{k=1}^Ky_{i,k}logp_{i,k}。\]
4.铰链损失
铰链损失(Hinge loss)一般用来使“边缘最大化”(maximal margin)。
铰链损失最开始出现在二分类问题中,假设正样本被标记为1,负样本被标记为-1,\(y\)是真实值,\(w\)是预测值,则铰链损失定义为:\[L_{Hinge}(w,y)=max\{1-wy, 0\}=\left|\right| 1-wy\left|\right|_+。\]然后被扩展到多分类问题,s假设\(y_w\)是对真实分类的预测值,\(y_t\)是对非真实分类预测中的最大值(我的理解:假设某物的标签是a类,分类问题中该物还可被预测为b类、c类,则\(y_w=Pr(a)\),\(y_t=max\{Pr(b),Pr(c)\}\)),则铰链损失定义为:\[L_{Hinge}(y_w,y_t)=max\{1+y_t-y_w,0\}。\]注意,二分类情况下的定义并不是多分类情况下定义的特例。
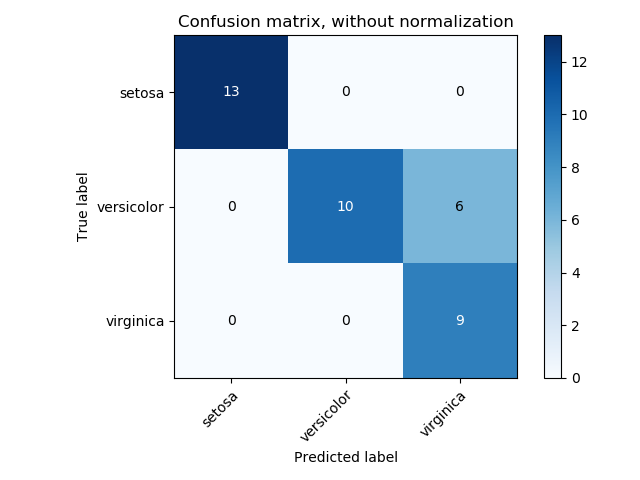
5.混淆矩阵
混淆矩阵(Confusion Matrix)又被称为错误矩阵,通过它可以直观地观察到算法的效果。它的每一列是样本的预测分类,每一行是样本的真实分类(反过来也可以),顾名思义,它反映了分类结果的混淆程度。混淆矩阵\(i\)行\(j\)列的原始是原本是类别\(i\)却被分为类别\(j\)的样本个数,计算完之后还可以可视化
6.kappa系数
kappa系数(Cohen's kappa)用来衡量两种标注结果的吻合程度,标注指的是把\(N\)个样本标注为\(C\)个互斥类别。计算公式为\[K={p_o-p_e\over 1-p_e}=1-{1-p_o\over 1-p_e}。\]其中\(p_o\)是观察到的符合比例,\(p_e\)是由于随机性产生的符合比例。当两种标注结果完全相符时,\(K=1\),越不相符其值越小,甚至是负的。
如,对于50个测试样本的二分类问题,预测与真实分布情况如下表:
| PREDICT | GROUND TRUTH | |
| 1 | 0 | |
| 1 | 20 | 5 |
| 0 | 10 | 15 |
7.准确率
准确率(Accuracy)衡量的是分类正确的比例。假设\(\widehat y_i\)是第\(i\)个样本预测类别,\(y_i\)是真实类别,在\(n_{sample}\)个测试样本上的准确率为\[accuracy={1\over n_{sample}}\sum_{i=1}^{n_{sample}}l(\widehat y_i=y_i)。\]其中\(l(x)\)是indicator function,当预测结果与真实情况完全相符时准确率为1,两者越不相符准确率越低。虽然准确率适用范围很广,可用于多分类以及多标签等问题上,但在多标签问题上很严格,在有些情况下区分度较差。在正负样本不平衡的情况下,准确率这个评价指标有很大的缺陷。比如在互联网广告里面,点击的数量很少,一般只有千分之几,如果用准确率,即使全部预测成负类(不点击)acc也有99%以上,没有意义。
8.海明距离
海明距离(Hamming Distance)用于需要对样本多个标签进行分类的场景。对于给定的样本\(i\),\(\widehat y_{ij}\)是对第\(j\)个标签的预测结果,\(y_{ij}\)是第\(j\)个标签的真实结果,\(L\)是标签数量,则\(\widehat y_i\)与\(y_i\)间的海明距离为\[D_{Hamming}(\widehat y_i, y_i)={1\over L}\sum_{j=1}^Ll(\widehat y_{ij}\not=y_{ij})。\]其中\(l(x)\)是indicator function。当预测结果与实际情况完全相符时,距离为0;当预测结果与实际情况完全不符时,距离为1;当预测结果是实际情况的真子集或真超集时,距离介于0到1之间。通过对所有样本的预测情况求平均得到算法在测试集上的总体表现情况,当标签数量\(L\)为1时,它等于1-Accuracy,当标签数\(L\gt 1\)时也有较好的区分度,不像准确率那么严格。
9.杰卡德相似系数
杰卡德相似系数(Jaccard similarity coefficients)也是用于需要对样本多个标签进行分类的场景。对于给定的样本\(i\),\(\widehat y_i\)是预测结果,\(y_i\)是真实结果,\(L\)是标签数量,则第\(i\)个样本的杰卡德相似系数为\[J(\widehat y_i, y_i)={\left|\right|\widehat y_i\bigcap y_i\left|\right|\over\left|\right|\widehat y_i\bigcup y_i\left|\right|}。\]它与海明距离的不同之处在于分母。当预测结果与实际情况完全相符时,系数为1;当预测结果与实际情况完全不符时,系数为0;当预测结果是实际情况的真子集或真超集时,距离介于0到1之间。通过对所有样本的预测情况求平均得到算法在测试集上的总体表现情况,当标签数量\(L\)为1时,它等于Accuracy。
10.多标签排序
更精细化的多标签分类效果衡量工具。设真实标签分类情况为\(y\in\{0,1\}^{n_{samples}\times n_{labels}}\),分类器预测情况为\(\widehat f\in\mathbb{R}^{n_{samples}\times n_{labels}}\)。
10.1涵盖误差
涵盖误差(Coverage error)计算的是预测结果中平均包含多少真实标签,适用于二分类问题。涵盖误差定义为\[coverage(y,\widehat f)={1\over n_{samples}}\sum_{i=1}^{n_{samples}}max_{j:y_{ij}=1}rank_{ij},\]其中\(rank_{ij}=\left|\right|\{k:\widehat f_{ik}\geq\widehat f_{ij}\left|\right|\)。可以看到它实际衡量的是真实标签中有多少排在预测结果的前面。
10.2标签排序平均精度
标签排序平均精度(Label ranking average precision)简称LRAP,它比涵盖误差更精细:\[LRAP(y,\widehat f)={1\over n_{samples}}\sum_{i=1}^{n_{samples}}{1\over\left|\right|y_i\left|\right|}\sum_{j:y_{ij}=1}{\left|\right| L_{ij}\left|\right|\over rank_{ij}},\]其中\(L_{ij}=\{k:y_{ik}=1,\widehat f_{ik}\geq\widehat f_{ij}\},rank_{ij}=\left|\right|\{k:\widehat f_{ik}\geq\widehat f_{ij}\}\left|\right|\)。
10.3排序误差
排序误差(Ranking loss)进一步精细考虑排序情况:\[ranking(y,\widehat f)={1\over n_{samples}}\sum_{i=1}^{n_{samples}}{1\over \left|\right|y_i\left|\right|(n_{labels}-\left|\right|y_i\left|\right|)}\left|\right|L_{ij}\left|\right|,\]其中\(L_{ij}=\{(k,l):\widehat f_{ik}\lt\widehat f_{ij},y_{ik}=1,y_{il}=0\}\)。
二、回归
拟合问题比较简单,所用到的衡量指标也相对直观。假设\(y_i\)是第\(i\)个样本的真实值,\(\widehat y_i\)是对第\(i\)个样本的预测值。
1.平均绝对误差
平均绝对误差MAE(Mean Absolute Error)又被称为\(l_1\)范数损失(l1-norm loss):\[MAE(y,\widehat y)={1\over n_{samples}}\sum_{i=1}^{n_{samples}}\left|\right|y_i-\widehat y_i\left|\right|。\]
2.平均平方误差
平均平方误差MSE(Mean Squared Error)又被称为\(l_2\)范数损失(l2-norm loss):\[MSE(y,\widehat y)={1\over n_{samples}}\sum_{i=1}^{n_{samples}}(y_i-\widehat y_i)^2。\]
3.解释变异
\[explained\ variance(y,\widehat y)=1-{Var\{y-\widehat y\}\over Var\{y\}}。\]
4.决定系数
决定系数(Coefficient of determination)又被称为\(R^2\)分数:\[R^2(y,\widehat y)=1-{\sum_{i=1}^{n_{samples}}(y_i-\widehat y_i)^2\over\sum_{i=1}^{n_samples}(y_i-\bar y)^2},\]其中\(\bar y={1\over n_{samples}}\sum_{i=1}^{n_{samples}}y_i\)。
三、聚类
1.兰德指数
兰德指数(Rand index)需要给定实际类别信息C,假设K是聚类结果,a表示在C与K中都是同类别的元素对数,b表示在C与K中都是不同类别的元素对数,则兰德指数为:\[RI={a+b\over C_2^{n_{samples}}}\]其中\(C_2^{n_{samples}}\)是数据集中可以组成的总元素对数,RI取值范围为[0,1],值越大意味着聚类结果与真实情况越吻合。
对于随机结果,RI并不能保证分数接近0。为了实现“在聚类结果随机产生的情况下,指标应该接近0”,调整兰德指数(Adjusted rand index)被提出,它具有更高的区分度:\[ARI={RI-E[RI]\over max(RI)-E[RI]}\],ARI取值范围为[-1,1],值越大意味着聚类结果与真实情况越吻合。从广义的角度来讲,ARI衡量的是两个数据分布的吻合程度。
2.互信息
互信息(Mutual Information)也是用来衡量两个数据分布的吻合程度。假设U与V是对N个样本标签的分配情况,则两种分布的熵(熵表示的是不确定程度)分别为:\[H(U)=\sum_{i=1}^{\left|\right| U\left|\right|}P(i)\ log(P(i)),H(V)=\sum_{j=1}^{\left|\right| V\left|\right|}P'(j)\ log(P'(j)),\]其中\(P(i)=\left|\right| U_i\left|\right|/N,P'(j)=\left|\right| V_j\left|\right|/N\)。U与V之间的互信息(MI)定义为:\[MI(U,V)=\sum_{i=1}^{\left|\right| U\left|\right|}\sum_{j=1}^{\left|\right| V\left|\right|}P(i,j)\ log({P(i,j)\over P(i)P'(j)}),\]其中\(P(i,j)=\left|\right| U_i\bigcap V_j\left|\right|/N\)。标准化后的互信息(Normalized mutual information)为:\[NMI(U,V)={MI(U,V)\over\sqrt{H(U)H(V)}}。\]与ARI类似,调整互信息(Adjusted mutual information)定义为:\[AMI={MI-E[MI]\over max(H(U),H(V))-E[MI]}。\]利用基于互信息的方法来衡量聚类效果需要实际类别信息,MI与NMI取值范围为[0,1],AMI取值范围为[-1,1],它们都是值越大意味着聚类结果与真实情况越吻合。
3.轮廓系数
轮廓系数(Silhouette coefficient)适用于实际类别信息未知的情况。对于单个样本,设\(a\)是与它同类别中其他样本的平均距离,\(b\)是与它距离最近不同类别中样本的平均距离,轮廓系数为:\[s={b-a\over max(a,b)}。\]对于一个样本集合,它的轮廓系数是所有样本轮廓系数的平均值。轮廓系数取值范围是[-1,1],同类别样本距离越相近且不同类别样本距离越远,分数越高。
四、信息检索
信息检索评价是对信息检索系统性能(主要满足用户信息需求的能力)进行评估的活动。通过评估可以评价不同技术的优劣,不同因素对系统的影响,从而促进本领域研究水平的不断提高。信息检索系统的目标是较少消耗情况下尽快、全面返回准确的结果。
IR的评价指标,通常分为三个方面:
(1) 效率(Efficiency)——可以采用通常的评价方法:时间开销、空间开销、响应速度。
(2) 效果(Effectiveness)——返回的文档中有多少相关文档、所有相关文档中返回了多少、返回得靠不靠前。
(3) 其他指标——覆盖率(Coverage)、访问量、数据更新速度
如何评价不同检索系统的效果呢?一般是针对相同的文档集合,相同的查询主题集合,相同的评价指标,不同的检索系统进行比较。相关的评测系统有:
(1) The Cranfield Experiments, Cyril W. Cleverdon, 1957-1968(上百篇文档集合)
(2) SMART System, Gerald Salton, 1964-1988(数千篇文档集合)
(3) TREC(Text Retrieval Conference), Donna Harman, 美国标准技术研究所,1992-(上百万篇文档),信息检索的“奥运会”
信息检索的评价指标分为两类:
(1) 对单个查询进行评估的指标:对单个查询得到一个结果
(2) 对多个查询进行评估的指标(通常用于对系统的评价):求平均
1.单个查询的评价指标
P&R
即分类问题中的召回率(信息检索领域称为查全率)和精确率(信息检索领域称为查准率)指标。相关文档是正样本,非相关文档是负样本,检索出的文档是预测分类为正的样本,信息检索问题转换为分类问题。\[查准率={检索出的相关信息量\over 检索出的信息总量}\]\[查全率={检索出的相关信息量\over 系统中的相关信息总量}\]
关于召回率的计算
(1)对于大规模语料集合,列举每个查询的所有相关文档是不可能的事情,因此,不可能准确地计算召回率
(2)缓冲池(Pooling)方法:对多个检索系统的Top N个结果组成的集合进行标注,标注出的相关文档集合作为整个相关文档集合。这种做法被验证是可行的,在TREC会议中被广泛采用。
虽然Precision和Recall都很重要,但是不同的应用、不同的用户可能对两者的要求不一样。因此,实际应用中应该考虑这点
(1) 垃圾邮件过滤:宁愿漏掉一些垃圾邮件,但是尽量少将正常邮件判定成垃圾邮件。
(2) 有些用户希望返回的结果全一点,他有时间挑选;有些用户希望返回结果准一点,他不需要结果很全就能完成任务。
F值和E值
(1) F值:召回率R和精确率P的调和平均值,if P=0 or R=0, then F=0 else \(F={2\over{{1\over R}+{1\over P}}}\),F值被称为F1值(F1 measure),因为recall和precision的权重一样。更通用的公式\(F_\beta\)如分类问题的精确率与召回率一节所示,其中F2值更重视召回率,F0.5值更重视精确率,都是常用的指标值。
(2) E值:召回率R和精确率P的加权平均值,\({1\over 2}\lt\alpha\lt 1\)表示更重视P。\[E=1-{1\over{\alpha\over P}+{1-\alpha\over R}}\]F和E的关系\[F=1-E,\ where\ \alpha={1\over 1+\beta^2}\]
P-R曲线
检索结果以排序方式排列,用户不可能马上看到全部文档,因此,在用户观察的过程中,精确率和召回率在不断变化,求出召回率分别为0%,10%,20%,30%,···,90%,100%上对应的精确率,然后描出图像。
假设某个查询q的标准答案集合为:Rq={d3,d5,d9,d25,d39,d44,d56,d71,d89,d123}
某个IR系统对q的检索结果如下:
| 1. d123 R=0.1, P=1 | 6. d9 R=0.3, P=0.5 | 11. d48 |
| 2. d84 | 7. d511 | 12. d48 |
| 3. d56 R=0.2, P=0.67 | 8. d129 | 13. d250 |
| 4. d6 | 9. d187 | 14. d113 |
| 5. d8 | 10. d25 R=0.4, P=0.4 | 15. d3 R=0.5, P=0.33 |
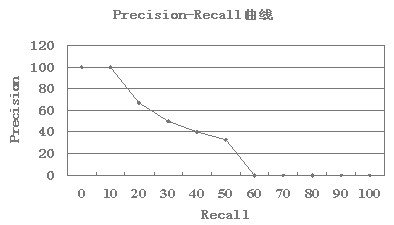
P-R曲线的插值问题,对于前面的例子,假设\(R_q=\{d3,d56,d129\}\)
(1) 3. d56 R=0.33,P=0.33; 8. d129 R=0.66,P=0.25; 15. d3 R=1,P=0.2
(2) 不存在10%,20%,\(\cdots\),90%的召回率,而只存在33.3%,66.7%,100%三个召回率点
(3) 在这种情况下,需要利用存在的召回率点对不存在的召回率点进行插值(interpolate)
(4) 对于t%,如果不存在该召回率点,则定义t%为从t%到(t+10)%中最大的正确率值
(5) 对于上例,0%,10%,20%,30%上正确率为0.33,40%~60%对应0.25,70%以上对应0.2
P-R曲线的优点:简单直接;既考虑检索结果的覆盖率,又考虑检索结果的排序情况
P-R曲线的缺点:单个查询的P-R曲线虽然直观,但是难以明确表示两个查询的检索结果的优劣
P-R曲线如何可以转化为单一指标呢?一般有两种方法:
(1) Break Point:P-R曲线上P=R的那个点。这样可以直接进行单值比较
(2) 11点平均正确率(11 point average precision):在召回率分别为0,0.1,0.2,\(\cdots\),1.0的十一个点上的正确率求平均,等价于插值的AP。
AP
平均正确率(Average Precision, AP):对不同召回率点上的正确率进行平均
(1) 未插值的AP:某个查询Q共有6个相关结果,某系统排序返回了5篇相关文档,其位置分别是第1,第2,第5,第10,第20位,则AP=(1/1+2/2+3/5+4/10+5/20+0)/6
(2) 插值的AP:在召回率分别为0,0.1,0.2,\(\cdots\),1.0的十一个点上的正确率求平均,等价于11点平均
(3) 只对返回的相关文档进行计算的AP,AP=(1/1+2/2+3/5+4/10+5/20)/5,倾向那些快速返回结果的系统,没有考虑召回率
不考虑召回率的话,单个查询评价指标还有:
(1) Precision@N:在第N个位置上的正确率,对于搜索引擎,考虑到大部分用户只关注前一、两页的结果,P@10,P@20对大规模搜索引擎非常有效
(2) NDCG:后面介绍
(3) Bpref:Binary preference,2005年首次引入到TREC的Terabyte任务中
NDCG
每个文档不仅仅只有相关和不相关两种情况,而是有相关度级别的,比如0,1,2,3.我们可以假设,对于返回结果:相关度级别越高的结果越多越好;相关度级别越高的结果越靠前越好。
NDCG(Normalized Discounted Cumulative Gain):计算相对复杂,对于排在位置n处的NDCG的计算公式:\[N(n)=Z_n\sum_{j=1}^n(2^{r(j)}-1)/log\ (1+j)。\]在MAP中,四个文档和query要么相关,要么不相关,也就是相关度非0即1.NDCG中改进了下,相关度分成从0到r的r+1的等级(r可设定)。当取r=5时,等级设定如下图所示:(应该还有r=1那一级,原文档有误,不过这里不影响理解。当然注意Value这一项,咱们可以直接定义分值,如0-3分值。求了2方实际上把Value的差异变大了,便于对比评测)
| Relevance Rating | Value(Gain) |
| Perfect | \(31=2^5-1\) |
| Excellent | \(15=2^4-1\) |
| Good | \(7=2^3-1\) |
| Fair | \(3=2^2-1\) |
| Bad | \(0=2^0-1\) |
| URL | Gain | Cumulative Gain | |
|---|---|---|---|
| #1 | http://abc.go.com/ | 31 | 31 |
| #2 | http://www.abcteach.com/ | 3 | 34=31+3 |
| #3 | http://abcnews.go.com/sections/scitech/ | 15 | 49=31+3+15 |
| #4 | http://www.abc.net.au/ | 15 | 64=31+3+15+15 |
| #5 | http://abcnews.go.com/ | 15 | 79=31+3+15+15+15 |
| #6 | ... | ... | ... |
| URL | Gain | Cumulative Gain | |
|---|---|---|---|
| #1 | http://abc.go.com/ | 31 | 31=31x1 |
| #2 | http://www.abcteach.com/ | 3 | 32.9=31+3x0.63 |
| #3 | http://abcnews.go.com/sections/scitech/ | 15 | 40.4=32.9+15x0.5 |
| #4 | http://www.abc.net.au/ | 15 | 46.9=40.4+15x0.43 |
| #5 | http://abcnews.go.com/ | 15 | 52.7=46.9+15x0.39 |
| #6 | ... | ... | ... |
| URL | Gain | Max DCG | |
|---|---|---|---|
| #1 | http://abc.go.com/ | 31 | 31=31x1 |
| #2 | http://abcnews.go.com/sections/scitech | 15 | 40.5=31+15x0.63 |
| #3 | http://www.abc.net.au/ | 15 | 48=40.5+15x0.5 |
| #4 | http://abcnews.go.com/ | 15 | 54.5=48+15x0.43 |
| #5 | http://www.abc.org/ | 15 | 60.4=54.5+15x0.39 |
| #6 | ... | ... | ... |
| URL | Gain | DCG | Max DCG | NDCG | |
|---|---|---|---|---|---|
| #1 | http://abc.go.com/ | 31 | 31 | 31 | 1=31/31 |
| #2 | http://www.abcteach.com/ | 3 | 32.9 | 40.5 | 0.81=32.9/40.5 |
| #3 | http://abcnews.go.com/sections/scitech/ | 15 | 40.4 | 48 | 0.84=40.4/48 |
| #4 | http://www.abc.net.au | 15 | 46.9 | 54.5 | 0.86=46.9/54.5 |
| #5 | http://abcnews.go.com/ | 15 | 52.7 | 60.4 | 0.87=52.7/60.4 |
| #6 | ... | ... | ... | ... | ... |
NDCG优点:图形直观,易解释;支持非二值的相关度定义,比P-R曲线更精确;能够反映用户的行为特征(如:用户的持续性persistence)
NDCG缺点:相关度的定义难以一致;需要参数设定。
Bpref
Bpref(Binary preference),2005年首次引入到TREC的Terabyte任务中。只考虑对返回结果列表中的经过判断后的文档进行评价。在相关性判断完整的情况下,Bpref具有与MAP相一致的评价结果。在测试集相关性判断不完全的情况下,Bpref依然具有很好的应用(比MAP更好)。这个评价指标主要关心不相关文档之前出现的次数。具体公式:\[Bpref={1\over R}\sum_r1-{|n ranked higher than r|\over R}\]其中,对每个topic,已判定结果中有R个相关结果。r是相关文档,n是Top R篇不相关文档集合的子集。(n ranked higher than r是指当前相关结果项之前有n个不相关的结果)。
举个例子说明Bpref的性能,假设检索结果集S为:
S={D1,D2,D3,D4,D5,D6,D7,D8,D9,D10}
其中D2,D5和D7是相关文档,D3和D4是未经判断的文档,R=3,Bpref=1/3[(1-1/3)+(1-1/3)+(1-2/3)]
2.多个查询的评价指标
多个查询的评价指标,一般就是对单个查询的评价进行求平均。平均的求法一般有两种:
(1) 宏平均(Macro Average):对每个查询求出某个指标,然后对这些指标进行算术平均
(2) 微平均(Micro Average):将所有查询视为一个查询,将各种情况的文档总数求和,然后进行指标的计算
例如:Micro Precision=(对所有查询检出的相关文档总数)/(对所有查询检出的文档总数)
宏平均对所有查询一视同仁,微平均受返回相关文档数目比较大的查询影响
宏平均和微平均的例子:
两个查询q1、q2的标准答案树木分别为100个和50个,某系统对q1检索出80个结果,其中正确数目为40,系统对q2检索出30个结果,其中正确数目为24,则:
P1=40/80=0.5,R1=40/100=0.4
P2=24/30=0.8,R2=24/50=0.48
MacroP=(P1+P2)/2=0.65
MacroR=(R1+R2)/2=0.44
MicroP=(40+24)/(80+30)=0.58
MicroR=(40+24)/(100+50)=0.43
MAP
MAP(Mean AP: Mean Average Precision): 对所有查询的AP求宏平均。具体而言,单个主题的平均精确率是每篇相关文档检索出后的精确率的平均值。主集合的平均精确率(MAP)是每个主题的平均精确率的平均值。MAP是反映系统在全部相关文档上性能的单值指标。系统检索出的相关文档越靠前(rank越高),MAP可能越高。如果系统没有返回相关文档,精确率默认为0.
多个查询下的查准率/查全率曲线,可通过计算其平均查准率得到,公式如下(Nq为查询的数量):\[MAP=\overline P(r)=\sum_{i=1}^{Nq}{Pi(r)\over Nq}\]P(r)是指查全率为r时的平均查准率,Pi(r)指查全率为r时的第i个查询的查准率
例如:假设有两个主题,主题1有4个相关网页,主题2有5个相关网页。某系统对于主题1检索出4个相关网页,其rank分别为1,2,4,7;对于主题2检索出3个相关网页,其rank分别为1,3,5.对于主题1,平均精确率为(1/1+2/2+3/4+4/7)/4=0.83。对于主题2,平均精确率为(1/1+2/3+3/5+0+0)/5=0.45。则MAP=(0.83+0.45)/2=0.64
MRR
MRR(Mean Reciprocal Rank): 对于某些IR系统(如问答系统或主页发现系统),只关心第一个标准答案返回的位置(Rank),越前越好,这个位置的倒数称为RR,对问题集合求平均,得到MRR。(把标准答案在被评价系统给出结果中的排序取倒数作为它的准确度,再对所有的问题取平均)
例子:两个问题,系统对第一个问题返回的标准答案的Rank是2,对第二个问题返回的标准答案的Rank是4,则系统的MRR为(1/2+1/4)/2=3/8
再举个例子:有3个query如下表(黑体为返回结果中最匹配的一项)
| Query | Results | Correct response | Rank | Reciprocal rank |
|---|---|---|---|---|
| cat | catten, cati, cats | cats | 3 | 1/3 |
| torus | torii, tori,toruses | tori | 2 | 1/2 |
| virus | viruses, virii, viri | viruses | 1 | 1 |
GMAP
GMAP(Geometric MAP): TREC2004 Robust任务引进先看一个例子:从MAP(宏平均)来看,系统A好于系统B,但是从每个查询来看,3个查询中有2个Topic B比A有提高,其中一个提高的幅度达到300%.
| 系统 | Topic | AP | Increase | MAP |
|---|---|---|---|---|
| 系统A | Topic1 | 0.02 | - | 0.113 |
| Topic2 | 0.03 | - | ||
| Topic3 | 0.29 | - | ||
| 系统B | Topic1 | 0.08 | +300% | 0.107 |
| Topic2 | 0.04 | +33.3% | ||
| Topic3 | 0.20 | -31% |
GMAP和MAP各有利弊,可以配合使用,如果存在高难度Topic时,GMAP更能体现细微差别。
3.面向用户的评价指标
前面的指标没有考虑用户因素,而相关不相关由用户判定。假定用户已知的相关文档集合为U,检索结果和U的交集为Ru,定义覆盖率(Coverage)C=|Ru|/|U|,表示系统找到的用户已知的相关文档比例。假定检索结果中返回一些用户以前未知的相关文档Rk,定义新颖率(Novelty Ratio)N=|Rk|/(|Ru|+|Rk|),表示系统返回的新相关文档的比例。
相对查全率:检索系统检索出的相关文档数量与用户期望得到的相关文档的数量的比例
查全努力:用户期望得到的相关文档与为了得到这些相关文档而在检索结果中审查文档数量的比率
4.评价指标总结
最基本的评价指标:召回率、精确率
不足:
1. 一些评价指标,如R-Precision, MAP, P@10等,都只考虑经过Pooling技术之后判断的相关文档的排序
2. 没有考虑判断不相关文档与文档未经判断的差别
3. 测试集越来越大,由于相关性判断基本上是人工判断,因此建立完整的相关性判断变得越来越难
参考链接:
本文创建于2021年10月19日10点28分,修改于2021年10月27日11点03分